Журнал «Травма» Том 14, №3, 2013

Введение

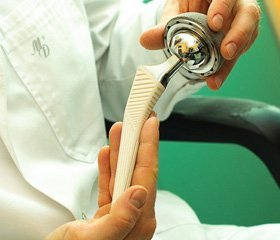
На современном этапе развития травматологии и ортопедии главным требованием к лечению переломов длинных костей и их последствий являются: стабильная фиксация, ранняя функция, отказ от внешней иммобилизации. Этим требованиям отвечает интрамедуллярный блокируемый остеосинтез [1–6]. Прочность современных фиксаторов позволяет надежно удержать отломки до наступления консолидации перелома при сохраненной функции смежных суставов. Стабильность остеосинтеза увеличивает межотломковая компрессия, что привлекает хирургов к ее использованию. Компрессионно-блокируемый фиксатор Блискунова представляет собой монолитный стержень из титанового сплава ВТ-16, в котором имеются круглые отверстия с резьбой для дистального и продолговатое безрезьбовое отверстие для проксимального блокирования (рис. 1А).

В проксимальном торце фиксатора находится отверстие для компрессирующего винта. Таким образом, внутрикостные фиксаторы Блискунова обладают всеми свойствами современных компрессионно-блокируемых фиксаторов и имеют преимущество за счет дистального блокирования через резьбовое соединение, что увеличивает стабильность остеосинтеза [1, 6, 7]. Разность же прочностных характеристик фиксатора и кости при выполнении неконтролируемой компрессии приводит к локальной деформации кости в области блокирующих элементов, к появлению напряженно-деформированного состояния фиксатора и блокирующих элементов, которое приближается к пределу их прочности. Широкое внедрение в последние десятилетия интрамедуллярного блокируемого остеосинтеза показало, что зачастую стабильная фиксация отломков «на операционном столе» в дальнейшем может приводить к появлению нестабильности, нарушению регенерации, излому металлоконструкции [3, 8, 9]. В связи с этим становится актуальным определение допустимых значений компрессии при использовании металлоконструкций, то есть задача расчета на прочность системы «металл — кость». В свою очередь, это требует изучения напряженно-деформированного состояния системы «металл — кость», которая представляет собой достаточно сложную биомеханическую конструкцию (рис. 1Б).

Цель исследования — определить допустимые значения компрессии при использовании внутрикостных компрессионно-блокируемых фиксаторов Блискунова.

Материалы и методы исследования

Для исследования напряженно-деформированного состояния конструкций использовались аналитические или численные расчеты, проводились натурные или модельные эксперименты.

Аналитические расчеты базировались на математических методах решения краевых задач, которые обычно сложны и трудоемки, а потому ограничены достаточно простыми геометрическими формами тел, граничными условиями и схемами нагружения. Проведение натурных экспериментов, требующих применения тех или иных датчиков нагрузки или деформации, в случае металлоостеосинтеза выполнить в клинических условиях практически невозможно. Сложность конструкции системы «фиксатор — кость», требующая рассмотрения поставленной задачи в трехмерной постановке, и значительное различие физико-механических свойств ее элементов делают проведение модельных экспериментов чрезвычайно сложным и дорогостоящим, а адекватность результатов, полученных на моделях, реальным значениям в натуре — весьма сомнительной.

Численные методы исследования напряженно-деформированного состояния конструкций не ограничены ни формой ее элементов, ни способом приложения нагрузки и позволяют варьировать в широких пределах физико-механические свойства элементов конструкций. С распространением и совершенствованием вычислительной техники все вышеперечисленное способствует их широкому применению для решения широкого спектра задач механики твердого деформируемого тела.

Исследование напряженно-деформированного состояния системы металлоостеосинтеза было выполнено на базе отдела деформирования и разрушения материалов НИИ проблем геодинамики Таврического национального университета им. В.И. Вернадского.

В основе любого расчета на прочность лежит расчетная схема, включающая в себя геометрию конструкции и действующие на нее нагрузки. В дальнейшем, в зависимости от конечных целей расчета, определяются напряжения и деформации элементов конструкции. Затем на основе анализа полей напряжений устанавливаются наиболее опасные сечения. При этом в зависимости от свойств материала и условий работы конструкции используются те или иные гипотезы прочности. Естественно, что при создании расчетной схемы сложной конструкции прибегают к некоторой идеализации ее формы, при этом степень этой идеализации влияет на достоверность результатов расчета.

Рассмотрим основные этапы численного исследования прочности конструкции: построение физической модели, построение математической модели, метод исследования математической модели и анализ полученных результатов. Построение физической модели включает в себя идеализацию свойств конструкции и внешних воздействий. В практических расчетах учесть все имеющиеся особенности конструкции, материала, формы, нагрузки невозможно. Приступая к практическим расчетам, приходится заменять реальные тела некоторыми идеализированными объектами — механическими моделями. Определенной идеализации подвергается также и понятие «внешние силы и нагрузки». Таким образом, физическая модель может быть наделена лишь частью свойств реальной конструкции, что приводит к упрощению ее математического описания. От того, насколько удачно выбрана физическая модель конструкции, зависит в итоге трудоемкость расчета и точность его результатов.

Следующим этапом расчета является математическое описание поведения модели, или построение математической модели. В общих чертах она включает в себя входные и выходные данные и математически сформулированный оператор перехода от первых ко вторым. При математическом описании поведения модели часто вводятся дополнительные упрощающие предположения о характере отдельных свойств модели и ее материала.

В результате воздействия на тело внешних нагрузок его точки могут переместиться относительно друг друга в новые положения. В этом случае вектор перемещения можно записать в виде   u = {u_x, u_y, u_z}, где   u_x, u_y, u_z — проекции вектора перемещений на координатные оси x, y, z соответственно. Разность перемещений двух соседних точек вызывает деформации в материале и связанные с ними напряжения. В общем случае линейные (E) и угловые (Y) деформации, а также нормальные (Q) и касательные (T) напряжения в материале состоят из шести компонентов:   E_x, E_y, E_z, _Yxy, Y_yz, Y_zx и   Q_x, _Qy, Q_z, T_xy, T_yz, T_zx. Для упругих изотропных материалов, которые идеализированно рассматриваются в поставленной физической задаче, имеем следующие соотношения между напряжениями и деформациями, определяемые законом Гука [10]:

где   E и G   — модули упругости и сдвига соответственно,  v — коэффициент Пуассона, G = E / 2(1 + v) .

Система уравнений, которым должны удовлетворять всюду в образце компоненты напряжений, включает уравнения равновесия

Соответствующие деформации   E_x, E_y, E_z, Y_xy, Y_yz, Y_zx должны удовлетворять уравнению совместности

причем деформации связаны с перемещениями следующими соотношениями:

Дополнительно к уравнениям (1) — (4) должны выполняться соответствующие граничные условия. Применительно к системе «фиксатор — кость» таковыми являются нижеприведенные.

На ненагружаемых поверхностях аппарата и кости поверхность материала свободна от напряжений, то есть

На контактных поверхностях «+» и «–» реализуется условие непрерывности нормальной составляющей вектора напряжений и условие скольжения без трения

где  Q_n; Qп — соответственно нормальные и касательные к контактной поверхности составляющие вектора напряжений.

Для решения поставленной краевой задачи используется сертифицированный численный метод конечных элементов (МКЭ), являющийся основой статического прочностного анализа программного комплекса ANSYS. Система «фиксатор — кость» разбивается на большое количество малых по размеру элементов, называемых конечными. Считается, что конечные элементы взаимодействуют между собой только в ограниченном количестве точек — эти точки называются узлами конечных элементов. Основная задача решения — найти неизвестные перемещения узлов конечных элементов. По известным перемещениям далее определяются деформации, а по деформациям — напряжения.

Физическая модель «фиксатор — кость»

В исследовании кость моделировалась, как показано на рис. 2, конической трубкой (1) длиной 320 мм с разрезом (2) посредине ее длины и перпендикулярно ее оси, моделирующим перелом кости.

Перпендикулярно оси трубки в каждой из ее частей для установки блокирующих винтов выполнялись по сквозному отверстию (3) диаметром 5 мм: одно — на 100 мм выше разреза, второе — на 100 мм ниже разреза. В месте установки верхнего блокирующего винта (4) внешний диаметр конической трубки составлял   D₁ = 24 мм, а внутренний диаметр —   d₁ = 15 мм. В месте установки нижнего блокирующего винта (5) внешний диаметр конической трубки составлял   D₂ = 20 мм, а внутренний диаметр —   d₂ = 12 мм. Блокирующие винты (4) и (5) моделировались цилиндрическими стержнями диаметром 5 мм и длиной 30 мм. На этом же рисунке показана используемая система координат xoy.

Внутрикостный фиксатор для металлоостеосинтеза моделировался в виде цилиндрического стержня (1) длиной 270 мм и диаметром 10 мм, как показано на рис. 3.

С одной стороны (верхней) вдоль его оси выполнялось на глубину 60 мм отверстие (2) диаметром 7 мм. С этой же стороны стержня в нем выполнялся сквозной паз (3) шириной 6 мм с закругленными краями на расстоянии 40–60 мм от торца стержня. С другой стороны (нижней) стержня перпендикулярно его оси выполнялось сквозное отверстие (4) диаметром 5 мм на расстоянии 10 мм от торца стержня.

Сборка системы «фиксатор — кость» проводилась в следующей последовательности:

— стержень (1) с отверстиями и пазом вводился в нижнюю часть трубки (2) до совпадения выполненных в них отверстий (3), как показано на рис. 4А;

— нижний блокирующий винт (4) вводился в отверстия (4) в трубке (2) и стержне (1), как показано на рис. 4Б;

— верхняя часть трубки (5) надевалась на часть стержня (1) с пазом;

— верхний блокирующий винт (6) вводился в отверстие (3) в трубке и в паз в стержне, как показано на рисунках 2 и 4В;

— компрессирующий винт (8) диаметром 7 мм вставлялся в отверстие (7) в верхней части трубки до касания им верхнего блокирующего винта (6), как показано на рис. 4В.

Задание компрессии для остеосинтеза моделировалось заданием смещения u_x компрессирующего винта (8) вдоль оси фиксатора в направлении нижнего блокирующего винта (4) при запрещении осевого смещения (u^a_x  = 0) верхнего торца (9) стержня (см. рис. 4А), моделирующего внутрикостный фиксатор. При этом верхний блокирующий винт (6) передает деформацию сжатия верхней (5) и нижней (2) частям трубки, моделирующей кость.

В свою очередь, нижняя часть трубки (2) через нижний блокирующий винт (4) передает деформацию растяжения на стержень (1), моделирующий фиксатор. В итоге стержень (1) оказывается в состоянии растяжения, а обе части трубки (5) и (2) — в состоянии сжатия, что и моделирует состояние компрессии при остеосинтезе. При этом компрессия будет возрастать с увеличением смещения u_x компрессирующего стержня (8), определяемого в натуре вращением компрессирующего винта. Поскольку натурный компрессирующий винт выполнен с шагом резьбы б = 1 мм/об, легко определить величину его смещения: u_x = nб, где n — количество оборотов нагружающего винта.

При моделировании системы металлоостеосинтеза физико-механические свойства ее элементов были приняты такими же, как и натурных элементов, которые представлены в табл. 1, с учетом того, что все элементы устройства для металлоостеосинтеза выполняются из титанового сплава ВТ-16.

В качестве критерия прочности был принят критерий по максимальным растягивающим или сжимающим напряжениям, соответствующий первой гипотезе прочности [14]:

где Q — действующее (расчетное) нормальное напряжение в элементе системы металлоостеосинтеза;   Q_в — предел прочности, при котором наступает предельное состояние, т.е. разрушение с образованием отдельностей или новых свободных границ, либо возникновение значительных остаточных деформаций.

Результаты и их обсуждение

Расчеты напряженно-деформированного состояния модели системы «фиксатор — кость» были проведены при величинах смещения нагружающего стержня 0,5 мм ≤ u_x  ≤ 2 мм. Очевидно, что областями, наиболее опасными с точки зрения прочности, в аппарате являются стенки паза, т.к. они имеют наименьшую площадь сечения, блокирующие винты, а в кости — зоны ее контакта с блокирующими винтами. Поэтому на рис. 5–7 приведены примеры результатов расчетов напряженно-деформированного состояния модели системы «фиксатор — кость» именно для этих областей. На этих рисунках результаты расчетов приведены в виде изополей нормальных напряжений   Q_x, действующих вдоль оси системы «фиксатор — кость», что достаточно наглядно показывает напряженное состояние ее элементов.

С целью оценки и анализа напряженного состояния элементов металлоостеосинтеза с учетом существенного различая их прочностных свойств при построении изополей напряжений _Qх использовались различные шкалы напряжений. При этом символы «Е + 09» или «Е + 10», указанные на рисунках в значениях единиц шкал после чисел, следует понимать как умножение соответствующих чисел на 10⁹ Па или 10¹⁰ Па. Наличие перед числами в значениях единиц шкал знака «–» означает действие сжимающих напряжений, а его отсутствие — растягивающих напряжений. Картины изополей напряжений _Qx в областях верхнего и нижнего блокирующих винтов системы металлоостеосинтеза в сечении хоу, проходящем через продольную ось системы, при различных значениях смещения нагружающего стержня u_x, рассчитанные в шкале напряжений, удобной для анализа напряженного состояния кости, приведены на рис. 5. Из представленной на рис. 5А картины изополей напряжений Q_x следует, что в кости в области ее контакта с верхним блокирующим винтом при u_x = 0,5 мм сжимающие напряжения не превышают 120 МПа, что составляет 0,75 от предела прочности кости на сжатие Q^К_в = 160 МПа. При увеличении значения   u_x до 1,0 мм (рис. 5В) в кости с ее внутренней стороны наблюдается на расстоянии 2,0–2,5 мм от верхнего блокирующего винта небольшая зона концентрации сжимающих напряжений глубиной ≈ 1 мм, в которой напряжения сжатия превышают величину Q^К_в. Эта зона захватывает лишь 18 % от площади сечения кости. Увеличение значения u_x до 1,5 мм приводит, как следует из рис. 5Д, к росту этой зоны до 50 % от площади сечения кости. Она наблюдается на расстоянии 1–6 мм от верхнего блокирующего винта и имеет глубину ≈ 2,5 мм. Из этого можно сделать вывод о том, что при смещении компрессирующего стержня u_x более чем на 1,5 мм (полтора оборота компрессирующего винта) будет происходить значительное смятие кости в области ее контакта с верхним блокирующим винтом. Из представленной на рис. 5Б картины изополей напряжений Q_x следует, что при u_x = 0,5 мм в кости в области ее контакта с нижним блокирующим винтом с ее внутренней стороны наблюдается на расстоянии 0–0,5 мм от блокирующего винта незначительная зона концентрации сжимающих напряжений глубиной ≈ 0,5 мм, в которой напряжения сжатия превышают величину Q^К_в. Эта зона захватывает около 1 % от площади сечения кости. При увеличении значения u_x до 1,0 мм (рис. 5Г) в кости с ее внутренней стороны происходит рост размеров этой зоны: она наблюдается на расстоянии 0–1,6 мм от нижнего блокирующего винта, имеет глубину около 0,5 мм и захватывает уже 40 % от площади сечения кости. Увеличение значения u_x до 1,5 мм приводит, как следует из рис. 5Е, к росту этой зоны до 58 % от площади сечения кости. Она наблюдается на расстоянии 0–3 мм от верхнего блокирующего винта и имеет глубину около 2,9 мм. Из этого можно сделать вывод о том, что при смещении нагружающего стержня u_x более чем на 1,0 мм будет происходить значительное смятие кости в области ее контакта с нижним блокирующим винтом. Из картин изополей напряжений Q_x, приведенных на рис. 5, следует, что величины напряжений сжатия в кости в области контакта с нижним блокирующим винтом значительно больше, чем в области контакта с верхним блокирующим винтом. Это легко объяснить различием приведенных ранее геометрических параметров кости в этих областях, в результате чего площадь сечения кости в месте установки верхнего блокирующего винта S₁ = П(D₁²  – d₁² )
больше площади сечения кости в месте установки нижнего блокирующего винта S₂ = П(D₂²  – d₂² ) в
     S₁     D₁²  – d₂¹

S₂ = D₂²  – d₂²  = 1,37 раза. 

Картины изополей напряжений Q_x в областях верхнего и нижнего блокирующих винтов системы металлоостеосинтеза в сечениях хоу и хоz, проходящих через продольную ось системы, при различных значениях смещения компрессирующего стержня u_x, рассчитанные в шкале напряжений, удобной для анализа напряженного состояния фиксатора, приведены на рис. 6 и 7 соответственно.

Из представленных на рис. 6 картин изополей напряжений Q_x следует, что при всех рассмотренных значениях смещения нагружающего стержня u_x и в верхнем, и в нижнем блокирующих винтах системы металлоостеосинтеза растягивающие напряжения ^QP_x не превышают 250 МПа, что составляет 0,25 от предела прочности титанового сплава ВТ-16 на растяжение   ^QТ_в   = 1050 МПа. Из картины изополей напряжений Q_x, приведенной на рис. 6А, 6В и 6Д следует, что при величинах смещения нагружающего стержня u_x, равных 0,5 мм, 1,0 мм и 1,5 мм, на внутренней стороне (поверхности) стенки паза фиксатора растягивающие напряжения Q^P_x   не превышают 500 МПа (что составляет 0,5 от Q^Т_в   ), 750 МПа (что составляет 0,75 от Q^Т_в   ) и достигают 1000 МПа (что практически равно значению ^QТ_в   ) соответственно.

Это же следует и из картин изополей напряжений   Q_x, представленных на рис. 7.

Следует отметить, что при смещении компрессирующего стержня u_x = 1,5 мм большая часть сечения стенки паза в фиксаторе оказывается под воздействием напряжений растяжения величиной ^QP_x    ≈ 1000 МПа (рис. 7В), практически равной значению предела прочности титанового сплава ВТ-16 на растяжение ^QТ_в   = 1050 МПа. На остальной небольшой части сечения стенки паза в фиксаторе действуют растягивающие напряжения ^QP_x   ≈ 1250 МПа, которые превосходят величину Q^Т_в   . Это означает, что при смещении нагружающего стержня u_x на 1,5 мм будет происходить разрушение устройства для металло­остеосинтеза.

Выводы

Анализ результатов расчетов напряженно-деформированного состояния модели системы «фиксатор — кость», проведенных для областей, наиболее опасных с точки зрения прочности при диаметре фиксатора 10 мм, диаметре блокирующих винтов 5 мм, диаметре компрессирующего винта — 7 мм, позволяет сделать следующие выводы.

1. Задание компрессии путем смещения компрессирующего винта более чем на 1,5 мм приводит к смятию кости в зоне более 50 % от площади сечения в области блокирующих элементов, что может в дальнейшем вызывать дестабилизацию системы «фиксатор — кость». Такое же значение компрессии приводит к созданию в стенках паза фиксатора напряжения, приближающегося к пределу прочности титанового сплава, а следовательно, может вызвать излом металлоконструкции.

2. Допустимым является задание компрессии путем смещения компрессирующего винта на величину до 1,0 мм, что соответствует одному его обороту после надежного введения в полный контакт отломков кости.

3. Исследование напряженно-деформированного состояния системы «фиксатор — кость» целесообразно провести для каждого типоразмера и дизайна фиксатора, что позволит исключить ряд технических осложнений и повысить качество остеосинтеза.