Мобильная версия

Журнал «» 5 (43) 2015

Применение интеллектуального анализа данных для классификации гемодинамических состояний

Авторы: Войтикова М.В., Войтович А.П. - Институт физики Национальной академии наук Беларуси; Хурса Р.В. - Кафедра поликлинической терапии Белорусского государственного медицинского университета

Рубрики: Кардиология

Разделы: Клинические исследования

Представлен новый метод классификации гемодинамических состояний c применением алгоритма интеллектуального анализа данных (машина опорных векторов) к медицинским измерениям артериального давления (АД). Коэффициенты линейной регрессии параметров АД (регрессионная модель гемодинамики) являются основой для составления шаблонов информации — библиотеки образцов кровообращения пациентов с известными гемодинамическими состояниями (артериальная гипертензия, гипотензия или нормотензия), которые используются для построения и обучения классификатора на основе машины опорных векторов. После предъявления классификатору вектора характерных особенностей АД тестируемого пациента, координаты которого представляют собой набор коэффициентов линейной регрессии систолического, диастолического и пульсового давления, происходит сравнение его с библиотекой образцов, по результатам которого дается заключение о гемодинамическом состоянии пациента. Объективной характеристикой гармоничного кровообращения является соблюдение требования о нахождении вектора характерных особенностей в определенных границах. Нарушение этого условия означает патологическое изменение гемодинамики сердечно-сосудистой системы, свойственное артериальной гипертензии, гипотензии или клинически латентным гемодинамическим нарушениям, которые характеризуются дисбалансом сердечной и сосудистой составляющих, обеспечивающих циркуляцию крови.

Представлений новий метод класифікації гемодинамічних станів із застосуванням алгоритму інтелектуального аналізу даних (машина опорних векторів) для медичних вимірювань артеріального тиску (АТ). Коефіцієнти лінійної регресії параметрів АД (регресійна модель гемодинаміки) є основою для складання шаблонів інформації — бібліотеки зразків кровообігу пацієнтів із відомими гемодинамічними станами (артеріальна гіпертензія, гіпотензія або нормотензія), які використовуються для побудови і навчання класифікатора на основі машини опорних векторів. Після пред’явлення класифікатору вектора характерних особливостей АД тестованого пацієнта, координати якого являють собою набір коефіцієнтів лінійної регресії систолічного, діастолічного і пульсового тиску, відбувається порівняння його з бібліотекою зразків, за результатами якого дається висновок про гемодинамічний стан пацієнта. Об’єктивною характеристикою гармонійного кровообігу є дотримання вимоги про знаходження вектора характерних особливостей у визначених межах. Порушення цієї умови означає патологічну зміну гемодинаміки серцево-судинної системи, властиву артеріальній гіпертензії, гіпотензії або клінічно латентним гемодинамічним порушенням, що характеризуються дисбалансом серцевої і судинної складових, що забезпечують циркуляцію крові.

This paper presents a new method for the classification of hemodynamic states with the application of data mining algorithms (support vector machine) to the medical measurements of blood pressure (BP). The coefficients of linear regression of BP parameters (the regression model of hemodynamics) are the basis for the patterns of information — library of blood circulation samples in patients with known hemodynamic states (hypertension, hypotension or normotension), which are used for the building and training the classifier based on support vector machines. After the presentation to the classifier of vector characteristics of the patient’s blood pressure, the coordinates of which are a set of coefficients of linear regression of systolic, diastolic and pulse pressure, there is a comparison of it with a library of samples, according to the results of which conclusion about hemodynamic condition of a patient is made. The objective characteristic of a harmonious circulation is a compliance with the requirements about vector of the characteristics staying within certain limits. Violation of this condition is a pathological change in the hemodynamics of the cardiovascular system, characteristic of arterial hypertension, hypotension or clinically latent hemodynamic disorders, which are characterized by an imbalance of cardiac and vascular components of circulating blood.

Ключевые слова

интеллектуальный анализ данных, регрессия, машина опорных векторов, гемодинамика.

інтелектуальний аналіз даних, регресія, машина опорних векторів, гемодинаміка.

data mining, regression, support vector machine, hemodynamics.

Статья опубликована на с. 36-42

Введение

Разработка и внедрение в медицину новых лабораторно-инструментальных методов исследования не только не заменяет традиционного клинического обследования пациентов, но и не решает основной проблемы: как из получаемой обширной информации сделать правильный диагностический вывод. Диагноз — это всегда вопрос вероятности, так как проявления одного и того же заболевания отличаются из-за индивидуальных особенностей пациента или не соответствуют классической картине болезни.

Важной проблемой кардиологии является артериальная гипертензия (АГ), которая часто вызывает диагностические затруднения, обусловленные существованием таких форм, как офисная гипертензия, маскированная гипертензия, и поэтому требует дополнительных обследований. Известна также гемодинамическая неоднородность АД, требующая индивидуального подхода к лечению [5]. Гипотензии как хроническому гемодинамическому нарушению в широкой практике уделяется мало внимания, но острые гипотензивные эпизоды представляют значительную опасность у реанимационного контингента пациентов со многими тяжелыми заболеваниями (сепсис, инфаркт миокарда, отравления и др.). Явным признакам нарушения гемодинамики в виде патологических изменений АД (гипертензия, гипотензия) предшествует период латентных нарушений кровообращения, что требует поиска способов распознавания подобных проблем со здоровьем на ранних этапах и в амбулаторных условиях.

Поэтому задача систематизации и формализации медицинской информации, в том числе в виде математических моделей, остается очень актуальной. Развитие медицинской кибернетики и современной вычислительной техники открывает для этого новые возможности.

В последние годы благодаря применению современных методов интеллектуального анализа данных Data Mining, действующих на основе правил, формализующих экспертные знания, стало возможным получение хороших результатов в медицинской диагностике [4]. В основу Data Mining положена концепция шаблонов [1], применяемых к различным данным для поиска клинически значимой информации. Используя алгоритмы Data Mining, при помощи таких шаблонов можно разработать базу знаний для моделирования в гемодинамике — науке, изучающей механизмы движения крови в сердечно-сосудистой системе.

Всесторонне оценить гемодинамику можно только по совокупности огромного количества показателей, получение многих из которых достижимо лишь при использовании сложной диагностической аппаратуры, что не всегда возможно в медицинской практике. Кроме того, понятие «гемодинамические параметры» имеет неодинаковый смысл в различных областях медицины. Для участкового терапевта оценка гемодинамики означает прежде всего исследование артериального давления и пульса, для оперирующих хирургов, анестезиологов-реаниматологов необходимы сведения о центральном венозном давлении, минутном объеме кровообращения и других параметрах, определение которых требует специальной аппаратуры и интервенционного вмешательства.

Учитывая, что распознавание латентных (доклинических) нарушений кровообращения, являющееся основой профилактического направления в кардиологии, относится к сфере первичного звена медицинской помощи (т.е. амбулаторно-поликлинической), в настоящей работе в качестве главного гемодинамического параметра, доступного для исследования, было избрано артериальное давление (АД).

Величина АД является интегральной характеристикой сердечно-сосудистой системы и зависит от объема циркулирующей крови, работы сердца и сосудов, реологических свойств крови и периферического сопротивления сосудов. АД характеризуется величинами систолического давления S (максимальное давление при сокращении сердечной мышцы), диастолического давления D (минимальное давление между ударами сердца в момент расслабления сердечной мышцы), а также пульсового давления W (по определению: W = S – D). Пульсовое давление W является барическим эквивалентом пульсового объема крови, поступающего в сосуд в систолу и покидающего его в диастолу, заключает в себе результат взаимодействия сократительной функции сердца, растяжимости артерий и величины волны отражения [6]. Несмотря на большие колебания внутрисосудистого давления во время систолы и диастолы, кровоток осуществляется при устойчивом режиме давления, которое называется средним гемодинамическим давлением. Это постоянная компонента АД, отражающая энергию непрерывного движения крови и зависящая от сократительной функции сердца и общего периферического сосудистого сопротивления, а также характеризующая компенсаторные возможности кровообращения [5, 6].

В исследованиях гемодинамики при суточном мониторировании АД ригидность кровеносных сосудов (т.н. амбулаторный индекс жесткости артерий AASI) предложено косвенно определять через коэффициенты линейной регрессии диастолического давления D по систолическому S, поскольку коэффициенты коррелируют со скоростью распространения пульсовой волны. Кроме того, показано, что значения этих коэффициентов могут служить предиктором инсульта и сердечно-сосудистой смертности как у гипертензивных, так и у нормотензивных пациентов [11, 12]. Увеличение жесткости артерий, приводящее к росту амплитуды волны отражения, обусловливает возрастание пульсового давления W, поэтому увеличенное W может служить предиктором повышенного риска смертности от сердечно-сосудистых заболеваний [15].

В процессе циркуляции крови пульсовое давление W является важным элементом. В частности, при рассмотрении величины АД как функциональной системы взаимодействующих параметров — систолического давления S («вход») и диастолического давления D («выход») с находящимся между ними пульсовым давлением W (W = S – D) последнее выступает в качестве состояния этой системы, а состояние, согласно теории функциональных систем П.К. Анохина [2], является системообразующим элементом. Временные ряды любых объектов (параметров, явлений), взаимодействующих в процессе деятельности функциональной системы, могут быть подвергнуты анализу с целью диагностики и прогноза функционирования данной системы. При этом важнейшими характеристиками функционального состояния системы являются не только сами взаимодействующие объекты, но и связи между ними [3]. Поэтому нахождение связей между параметрами АД может быть использовано для построения регрессионной модели кровообращения, представленной как взаимодействие систолической и диастолической составляющих этого процесса и характеризующей функционирование сердечно-сосудистой системы в процессе продвижения крови. Линейное регрессионное моделирование легло в основу патентованной методики количественного анализа связей параметров АД с пульсовым давлением W в качестве аргумента, а найденные связи (коэффициенты регрессии) использованы для диагностики гомеостатического типа гемодинамики согласно предложенной классификации, которая может быть использована для раннего распознавания гемодинамических нарушений (т.е. дисбаланса сердечно-сосудистого взаимодействия в процессе продвижения крови) [9, 10].

В вышеизложенном контексте применение алгоритмов Data Mining, в частности машины опорных векторов, к результатам регрессионного моделирования по параметрам АД представляется перспективным для трансформации сырых данных АД в новую клиническую информацию — идентификацию состояний кровообращения пациентов по индивидуальным гемодинамическим функциям, характеризующим взаимодействие сердца и сосудов в процессе продвижения крови, и функциональную диагностику нарушений кровообращения, в том числе клинически латентных.

Построение линейной регрессионной модели

Очевидно, что при рассмотрении взаимосвязей между S и W (или D и W) переменная S представляется независимой, а W — зависимой, но такая зависимость является неоднозначной в том смысле, что каждому конкретному значению S может соответствовать некоторое вероятностное распределение зависимой переменной W. Поэтому математическое ожидание переменной определяет функцию регрессии S на W, D на W или S на D.

Суть линейной регрессии состоит в следующем. Для множества измерений АД строится линейная модель S = Q + aW с постоянными коэффициентами Q и a с использованием метода наименьших квадратов для минимизации ошибки аппроксимации. Коэффициент Q здесь имеет смысл значения беспульсового давления [9] (давление в области затухающей пульсовой волны в конечной части артериол). Поскольку пульсовое давление определяется как W = S – D, то получаем D = Q + (a – 1)W. Аналогично строится уравнение регрессии систолического давления на диастолическое: S = B + AD, где параметры А и В составляют второй набор коэффициентов линейной регрессии параметров АД. Таким образом, линейными уравнениями регрессии S = Q + aW и D = Q + (a – 1)W можно описать кровообращение в пространстве параметров АД.

Величина параметра а косвенно определяет соотношение систолической и диастолической составляющих процесса кровообращения, т.е. отражает участие собственно пропульсивной работы сердца в обеспечении циркуляции крови (что происходит в период систолы) и участие сосудов в дальнейшем продвижении крови в период диастолы, обеспечиваемом их упругоэластическими свойствами (так называемое периферическое сердце). Это соотношение можно использовать для классификации гемодинамических состояний.

Гармонический тип кровообращения, который предполагает, что D < S, 0 < a < 1, означает нормальное сердечно-сосудистое взаимодействие в процессе продвижения крови, при котором участие сердца (его вклад) обеспечивает большую часть работы по циркуляции крови, а участие сосудов, соответственно, меньшую. Значение параметра a < 1 в линейном уравнении D = Q + (a – 1)W указывает на возникновение противоположно направленной составляющей в диастолическом давлении (т.н. диастолическая дисфункция кровообращения [9]). Дисфункциональный диастолический тип гемодинамики означает нарушение диастолической составляющей процесса кровообращения, которое осуществляется только силой сокращения –миокарда, при этом сосуды не помогают кровотоку. Снижение величины систолического давления S до уровня беспульсового давления Q и ниже при a ≤ 0 также представляет нарушение гемодинамики сердечно-сосудистой системы из-за противоположно направленной составляющей в систолическом давлении, что по аналогии можно назвать систолической дисфункцией кровообращения. При этом типе гемодинамики кровообращение осуществляется главным образом за счет сосудов (и отчасти периферических мышц, т.е. периферического сердца), а также объема циркулирующей крови [9].

Следует отметить, что гармонический тип гемодинамики наблюдается не только у здоровых людей, поскольку гармоничное взаимодействие сердца и сосудов может сопровождаться разной величиной давления Q (например, в начальных стадиях АГ значение Q чрезмерно низкое или высокое). По этой причине классификация типов кровообращения пациента не должна быть ограничена только пороговыми значениями единственного параметра а. Так, определенным прогностическим потенциалом в задаче классификации гемодинамики обладает полный набор коэффициентов линейной регрессии временного ряда измерений АД [17]. Каждый из этих коэффициентов имеет свой биофизический смысл. Величина Q характеризует давление потока крови в области затухающей пульсовой волны. Показано, что при нормальном (гармоническом) типе кровообращения величина коэффициента Q практически совпадает со значением среднего гемодинамического давления (постоянная компонента АД, как отмечено выше), являющегося интегрированным средним значением АД за время сердечного цикла [8]. Параметр а определяет соотношение вкладов сердца и сосудов в процесс кровообращения. Значения коэффициентов A и B, определяющие линейную регрессию систолического S на диастолическое давление D, могут быть также определены в терминах индекса жесткости сосудов AASI [12]. Кроме того, было сделано наблюдение о связи возникновения гипертонического криза со значениями параметров А и В [10].

Перспективным классификатором гемодинамики представляется Support Vector Machine (SVM, или машина опорных векторов) — алгоритм Data Mining, основанный на обучении на примерах (библиотеке образцов), использующий разделение объектов в пространстве признаков с помощью гиперплоскости, которая максимально разделяет векторы характерных признаков объектов, принадлежащих к разным классам (координаты вектора описывают отдельные атрибуты объекта) [16]. Среди разнообразия современных алгоритмов Data Mining метод SVM признан одним из эффективных алгоритмов, имеющим простую математическую постановку задачи и, в отличие от нейронных сетей, не страдающим от переобучения (т.е. влияния частных закономерностей в обучающей выборке) [1].

Создание классификатора гемодинамических состояний по параметрам АД на основе SVM в настоящем исследовании предполагало его обучение на библиотеке образцов АД пациентов, которые заведомо принадлежат к одному из классов: артериальная гипертензия, гипотензия, нормальное АД (обучающая выборка) с последующей классификацией рядов АД пациентов контрольной выборки. Такой классификатор может обеспечить качественную классификацию гемодинамических состояний пациента по параметрам АД без априорных знаний о здоровье пациента, поскольку работает с векторной моделью представления временного сигнала АД (в общем случае произвольной частоты дискретизации, длительности измерения АД, с пропусками измерений).

Таким образом, задача классификации гемодинамического состояния пациента состоит в применении алгоритма SVM к параметрам регрессионного моделирования временных рядов АД и в определении принадлежности его гемодинамики к одному из трех классов, характеризующих кровообращение при артериальной гипертензии, нормотензии или гипотензии.

Обучение машины опорных векторов и классификация образцов АД

Изучались ряды величин АД пациентов в дневное время с интервалом измерений через 15 мин и длительностью не менее 6 часов при помощи аппаратных средств для суточного мониторирования АД (СМАД) серии BPLab (Россия) [7]. Группу лиц с впервые выявленной артериальной гипертензией (АГ) составили 50 пациентов: 24 женщины и 26 мужчин в возрасте 19–59 (32,7 ± 9,8) лет. Среднее АД (M ± SD) в группе за период наблюдения для S составило 140,6 ± 8,0 мм рт.ст., для D — 87,2 ± 12,6 мм рт.ст. Практически здоровые лица в количестве 121 человека, среди которых было 57 мужчин и 64 женщины в возрасте 18–48 (23,8 ± 5,1) лет, составили группу нормотензивных пациентов. Среднее АД за период наблюдения в этой группе для S составило 121,1 ± 8,6 мм рт.ст., для D — 72,7 ± 5,5 мм рт.ст.

Также была использована электронная база данных MIMIC II Clinical Database [14]. В данной базе изучены временные ряды АД 43 пациентов отделения интенсивной терапии с вторичной гипотонией, развившейся на фоне тяжелых основных заболеваний разной этиологии (посттравматическая легочная недостаточность, инфаркт миокарда, сердечная недостаточность и др.), пережившие хотя бы один эпизод острой гипотензии: 21 мужчина в возрасте 22–90 (64,3 ± 20,4) лет, 22 женщины в возрасте 60–90 (74,8 ± 12,5) лет (группы H1, H2, C2 с высоким риском вторичной гипотонии MIMIC II Clinical Database [14]). Для унификации данных частота дискретизации АД-сигналов базы данных MIMIC II Clinical Database была увеличена до одного измерения в 15 мин.

Ввиду различия величин систолического и диастолического давления при разных способах измерения статистический анализ данных АД, полученных разными способами, следует признать некоррект–ным. Нами было установлено, что удаление отдельных измерений или изменение частоты дискретизации ряда АД практически не влияет на вычисляемые коэффициенты. Это означает, что при регрессионном моделировании соотношения между параметрами АД не зависят от способа его измерения, поэтому сравнительный анализ параметров моделирования может быть проведен для всех имеющихся данных. Все сигналы АД подвергались усреднению посредством сглаживания при скользящем среднем, к каждому ряду сигналов было применено регрессионное моделирование и определен вектор атрибутов с координатами, равными коэффициентам линейной регрессии.

Разделение общей базы данных АД (214 пациентов) на обучающую и контрольную выборки проводилось случайным образом в пропорции 75/25 % (160 и 54 пациента) соответственно.

Поскольку, как отмечено выше, каждый из коэффициентов регрессии имеет свой биофизический смысл, то алгоритм SVM можно применить к любому сочетанию параметров (Q, a, A, B), что позволяет получить 2, 3 и 4-мерные классификаторы. Сокращение числа значимых входных признаков (уменьшение размерности вектора характерных особенностей) является важной задачей классификации, поскольку удаляются менее значимые признаки при упрощении модели и улучшении ее качества. Ранжирование признаков в настоящей работе проводилось по ROC-критерию (Receiver Operating Characteristics), который устанавливает зависимость числа верно классифицированных образцов от числа неверно классифицированных для каждого признака. Применение ROC-критерия к компонентам вектора x позволило в итоге понизить размерность вектора до 2: x = (Q, a).

Критериями выбора классификатора на основе (Q, a) были качество классификации (число верно/неверно классифицированных образцов), наглядность (максимальное разделение образцов в пространстве) и простота (преимущество 2-мерной классификации). Применение алгоритма SVM к другой естественной паре (A, B)

дало приблизительно такое же качество разделения образцов, но наглядность карты (A, B) была хуже.

Задача построения разделяющей SVM-классифицирующей функции эквивалентна нахождению единственного минимума квадратичного функционала, когда суммирование осуществляется только по опорным векторам x0, лежащим ближе всех к разделяющей гиперплоскости.

После выбора классификатора составлялась библиотека образцов: к каждому ряду АД было применено регрессионное моделирование и определен вектор атрибутов с координатами, равными коэффициентам линейной регрессии x = (Q, a), затем векторы наносились на карту параметров Q и a. Поскольку каждый сигнал АД представляется как вектор в пространстве признаков и принадлежит только к одному из рассматриваемых классов — артериальная гипертензия, гипотензия или нормотензия, то максимизация зазора между классами означает более достоверную классификацию. SVM строит классифицирующую функцию при непрерывном уменьшении эмпирической ошибки классификации объектов, при этом обучение SVM-классификатора считается завершенным при достижении максимального значения показателя качества разделения образцов.

Классификация гемодинамики пациентов конт–рольной выборки на основе 2-мерного вектора атрибутов (Q и a) и линейной решающей функции дала высокий показатель качества разделения сигналов — 96 %.

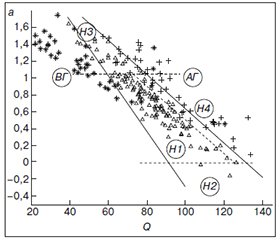
Рис. 1 демонстрирует основную идею SVM при линейной разделимости объектов. На рис. 1 звездочками помечены образцы АД пациентов со вторичной гипотензией (область ВГ), треугольниками — нормотензивных пациентов (область Н) и крестиками — пациентов с артериальной гипертензией (область АГ), линейные решающие функции отмечены сплошной прямой.

Уравнения линейных решающих функций (границы раздела) образцов пациентов со вторичной гипотензией (ВГ) и нормотензивных пациентов (Н1-Н4), а также нормотензивных пациентов (Н1-Н4) и пациентов с АГ имеют вид: a = –0,03Q + 3,03 и a = –0,02Q + 2,65.

В части расположения нормотензивных образцов (область Н1-Н4) рис. 1 следует дополнить двумя пороговыми линиями (отмечены пунктиром): на уровне а = 0 (разделение подгруппы Н1 с гармоническим кровообращением и подгруппы Н2 с систолическим дисфункциональным кровообращением в соответствии с терминологией работы [7]) и на уровне а = 1 (разделение подгруппы Н1 и подгруппы Н3 с диастолическим дисфункциональным кровообращением, где а > 1). Таким образом, группа нормотензивных пациентов, согласно пороговым значениям параметра а, распадается на 3 подгруппы: Н1, Н2, Н3, где Н1 ограничена пороговыми значениями а сверху и снизу (рис. 1).

На рис. 1 видно, что множества АГ и Н перекрываются в области, обозначенной Н4, поэтому формально среди нормотензивных пациентов можно выделить подгруппу Н4, которая, с одной стороны, характеризуется гармоническим кровообращением (0 < а < 1), с другой стороны, в эту область параметров равновероятно попадает ряд образцов АД пациентов с артериальной гипертензией. Можно предположить, что подгруппа Н4 представляет пациентов с повышенным риском развития АГ, поскольку характеризуется параметрами кровообращения, свойственными пациентам с АГ. С учетом перекрытия Н4 область истинно гармонического кровообращения Н1 (рис. 1) имеет вид: –0,03Q + + 3,03 < a < –0,02Q + 2,52.

Кроме того, в популяции нормотензивных пациентов выделяется подгруппа Н3 с дисфункциональным диастолическим типом кровообращения, т.к. а > 1 (область Н3 на рис. 1), а также малочисленная группа лиц с дисфункциональным систолическим типом, т.к. а < 0 (область Н2 на рис. 1). Можно предположить, что нормотензивные пациенты из подгруппы Н3, гемодинамика которых характеризуется нарушением диастолической составляющей процесса кровообращения, осуществляемого только усилиями миокарда, без помощи сосудов, также нуждаются в дальнейшем мониторинге, поскольку в долгосрочной перспективе данные пациенты могут перейти в группу гипертоников (группа АГ на рис. 1), а далее, в результате прогрессирования патологического процесса и ослабления миокарда, переместиться в подгруппу Н2 (систолический дисфункциональный тип) из-за псевдонормального состояния подгруппы Н1.

Рис. 1 показывает также пример гемодинамики пациентов со вторичной гипотонией (область ВГ) на фоне тяжелого основного заболевания. Для этих пациентов характерна диастолическая дисфункция кровообращения и низкое давление в области затухающей пульсовой волны (а > 1, Q < 70 мм рт.ст.). Для группы пациентов с артериальной гипертензией (область АГ) перестройка гемодинамики означает повышенное значение Q (т.е. повышенное давление в конечной части артериол) при значениях параметра а > 0. При этом у одной части пациентов с АГ имеется гармоничное кровообращение (0 < a < 1), а у другой — дисфункционально-диастолическое кровообращение. Такая разная организация кровообращения предполагает разные подходы к лечению этих пациентов.

Заключение

В настоящем исследовании предложена классификация гемодинамических состояний с применением интеллектуального анализа данных. В основе классификации лежит применение обученного на примерах машинного алгоритма дифференциации сигналов по методу опорных векторов, использующего вектор характерных особенностей артериального давления, координаты которого представляют собой набор коэффициентов линейной регрессии систолического, диастолического и пульсового давления.

Определена функциональная характеристика гармоничного кровообращения (адекватного нормальной физиологии взаимодействия сердца и сосудов в процессе продвижения крови), которая заключается в нахождении коэффициентов линейной регрессии систолического, диастолического на пульсовое давление в определенных границах: –0,03Q + 3,03 < а < –0,02Q + 2,52 при 0 < а < 1. Расположение коэффициентов линейной регрессии вне этих границ указывает на патологическое изменение гемодинамики сердечно-сосудистой системы, в том числе свойственное артериальной гипертензии или, наоборот, гипотензии, которое сопровождается как нормальным, так и диспропорциональным вкладом сердца и сосудов в обеспечение циркуляции крови (дисфункциональная гемодинамика).

Нормотензивные пациенты с параметрами регрессии в пограничных с гипотензивными и гипертензивными пациентами областях составляют группу риска развития патологического типа кровообращения даже при гармоническом вкладе сосудов и сердца в крово–обращение. Кроме того, в популяции нормотензивных пациентов выделяются подгруппы лиц с диспропорциональным участием сердца и сосудов в обеспечении циркуляции крови: с гипертрофированным вкладом сердца — диастолическое дисфункциональное крово–обращение, с гипертрофированным вкладом сосудов — систолическое дисфункциональное кровообращение. Такая организация гемодинамики позволяет отнести их также к категории лиц повышенного риска развития сердечно-сосудистых заболеваний, в первую очередь АГ, поскольку у них имеются клинически латентные нарушения кровообращения. Поэтому использование предлагаемого метода в клинической медицине позволит выявить среди нормотензивных пациентов группу риска развития АГ, что указывает на необходимость их дальнейшего наблюдения.

Таким образом, применение алгоритма интеллектуального анализа данных к параметрам линейного регрессионного моделирования параметров АД открывает новые возможности для идентификации индивидуальных особенностей кровообращения, включая диагностику нарушений сердечно-сосудистого взаимодействия в процессе продвижения крови, в том числе клинически латентных. Результатом использования предложенного классификатора является отнесение гемодинамики пациента к следующим классам: артериальная гипертензия, артериальная гипотензия, гармоническая гемодинамика, повышенный риск АГ, латентные гемодинамические нарушения (дисфункциональные диастолический или систолический типы кровообращения). Использование предложенного метода в процессе динамического наблюдения пациентов открывает дальнейшие перспективы для разработки методов раннего выявления угрожающих здоровью тенденций гемодинамики и сердечно-сосудистых заболеваний.

Список литературы

1. Андрейчиков А.В., Андрейчикова О.Н. Интеллектуальные информационные системы. — М.: Финансы и статистика, 2006. — 424 c.

2. Анохин П.К. Узловые вопросы теории функциональной системы. — М.: Наука, 1980. — 197 с.

3. Анохин П.К. Узловые вопросы теории функциональной системы. — М.: Наука, 1980. — 197 с.

4. Баевский Р.М. Прогнозирование состояний на грани нормы и патологии. — М.: Медицина, 1979. — 298 с.

5. Кузнецова А.В., Сенько О.В. Возможности использования методов Data Mining при медико-лабораторных исследованиях для выявления закономерностей в массивах данных // Врач и информационные технологии. — 2005. — № 2.

6. Кушаковский М.С. Гипертоническая болезнь. — СПб.: Сотис,1995. — 4-е изд. — 32 c.

7. Рашмер Р. Динамика сердечно-сосудистой системы / Пер. с англ. М.А. Безносовой, Т.Е. Кузнецовой; Под ред. Г.И. Косицкого. — М.: Медицина, 1981. — 600 c.

8. Суточный мониторинг артериального давления BPLab: http:// www.bplab.ru

9. Хурса Р.В. Непульсирующий компонент артериального давления при разных способах определения и новые гемодинамические характеристики // Артериальная гипертензия и профилактика сердечно-сосудистых заболеваний. Материалы VI Международной конференции. — Витебск: ВГМУ, 2011. — C. 83-87.

10. Хурса Р.В., Чеботарев В.М. Гемодинамические детерминанты гомеостаза сердечно-сосудистой системы // Клиническая физиология кровообращения. — 2007. — № 4. — С. 71-77.

11. Чеботарев В.М., Хурса Р.В., Балышева В.М. Способ перманентного контроля индивидуального функционального состояния кровообращения: Патент BY № 4876.

12. Benetos A., Lacolley P. From 24-Hour Blood Pressure Measurements to Arterial Stiffness: A Valid Short Cut? // Hypertension. — 2006. — Vol. 47. — P. 327-328.

13. Dolan E., Thijs L., Li Y. et al. Ambulatory arterial stiffness index as a predictor of cardiovascular mortality in the Dublin Outcome Study // Hypertension. — 2006. — Vol. 47. — P. 365-370.

14. Saeed M., Villarroel M., Reisner A.T. et al. Multiparameter intelligent monitoring in intensive care II (MIMIC-II): A public-access ICU database // Critical Care Medicine. — 2011. — Vol. 39 (5). — P. 952-960.

15. The MIMIC II Project database: http:// physionet.org/physiobank/database/mimic2db

16. Thomas F., Blacher J., Benetos A. et al. Cardiovascular risk as defined in the 2003 european blood pressure classification: the assessment of an additional predictive value of pulse pressure on morta–lity // J. Hypertens. — 2008. — Vol. 26 (6). — P. 1072-1077.

17. Vapnik V. Statistical learning theory. — Berlin: Springer, 1998. — 732 p.

18. Voitikova M.V., Khursa R.V. Linear regression in hemodynamics // Nonlinear Phenomena in Complex Systems. — 2012. — Vol. 15, № 2. — P. 203-206.

Впервые опубликовано в журнале «Врач и информационные технологии». 2013. № 1. С. 32-41