Мобильная версия

Журнал «Травма» Том 18, №6, 2017

Компьютерное моделирование эндопротезирования тазобедренного сустава с использованием трабекулярно-бионического бедренного компонента Рhysiohip

Авторы: Бондарь В.К.(1), Косяков А.Н.(1), Бурьянов А.А.(2), Hindenlang Ulrich(3), Schneider Ralf(4)
(1) — Киевский городской центр эндопротезирования, хирургии и реабилитации, КГКБ № 12, г. Киев, Украина
(2) — Национальный медицинский университет им. А.А. Богомольца, г. Киев, Украина
(3) — LASSO Ingenieurgesellschaft mbH, Leinfelden-Echterdingen, Germany
(4) — HLRS High Performance Computing Center Stuttgart, Stuttgart, Germany

Рубрики: Травматология и ортопедия

Разделы: Клинические исследования

Найбільш частою причиною ревізійного ендопротезування є асептична нестабільність компонентів. Розробки щодо попередження подібних ситуацій полягають у вдосконаленні конструкцій ендопротезів, застосуванні матеріалів з механічними характеристиками, близькими до властивостей кістки. У статті надано результати коротко- і довгострокового прогнозування наслідків імплантації трабекулярно-біонічного стегнового компонента Physiohip ендопротеза кульшового суглоба при комп’ютерному моделюванні. Виконано об’ємне моделювання та кінцево-елементний аналіз взаємодії кістки з імплантатом в умовах фізіологічного навантаження. Механічні властивості кістки описані моделлю неоднорідного ортотропного середовища, параметри якого визначаються шляхом обробки даних комп’ютерної томографії. Отримано чисельні дані про напружений стан і розподіл енергії деформації кістки в зоні протезування. Результат передачі навантаження на кістку через ніжку ендопротеза Physiohip при довгостроковій стабілізації близький до фізіологічного. Ці відомості дають підстави вважати трабекулярно-біонічну ніжку досить ефективним засобом ендопротезування кульшового суглоба.

Наиболее частой причиной ревизионного эндопротезирования является асептическая нестабильность компонентов. Разработки по предупреждению подобных ситуаций заключаются в совершенствовании конструкций эндопротезов, применении материалов с механическими характеристиками, близкими к свойствам кости. В статье представлены результаты кратко- и долгосрочного прогнозирования последствий имплантации трабекулярно-бионического бедренного компонента Physiohip эндопротеза тазобедренного сустава при компьютерном моделировании. Выполнено объемное моделирование и конечно-элементный анализ взаимодействия кости с имплантатом в условиях физиологического нагружения. Механические свойства кости описаны моделью неоднородной ортотропной среды, параметры которой определяются путем обработки данных компьютерной томографии. Получены численные данные о напряженном состоянии и распределении энергии деформации кости в зоне протезирования. Результат передачи нагрузки на кость через ножку эндопротеза Physiohip при долгосрочной стабилизации близок к физиологическому. Эти сведения дают основания считать трабекулярно-бионическую ножку довольно эффективным средством эндопротезирования тазобедренного сустава.

The most frequent causes for revision of endoprosthetics are aseptic instabilities of the components. Researches to prevent such instabilities are being carried out improving the designs of endoprostheses, application of materials with mechanical cha-racteristics close to those of bone. This article covers the results of both short- and long-term implantation of trabecular-bionic femoral Physiohip component in a hip joint endoprosthesis using computer simulations. 3D modeling and finite element analysis of the interactions between the bone and the implant under conditions of physiological stress were performed. The mechanical properties of bone are described using the inhomogeneous orthotropic medium model, the parameters of which are determined by analyzing data from a computed tomography. Numerical data on the stress state and the distribution of bone deformation energy in the prosthetic zone are collected. The results of transferring the load to the bone through the stem of the Physiohip endoprosthesis with long-term stabilization are close to physiological. This research shows trabe-cular-bionic stem as an effective means of endoprosthetics of the hip joint.

Ключевые слова

ендопротез кульшового суглоба; трабекулярно-біонічна ніжка Physiohip; кінцево-елементний аналіз; фізіологічне навантаження; неоднорідне ортотропне середо-вище; комп’ютерна томографія; напружений стан; енергія деформації

эндопротез тазобедренного сустава; трабекулярно-бионическая ножка Physiohip; конечно-элементный анализ; физиологическое нагружение; неоднородная ортотропная среда; компьютерная томография; напряженное состояние; энергия деформации

hip prosthesis; trabecular-bionic stem Physiohip; finite element analysis; physiological loading; heterogeneous orthotropic medium; computed tomography; stress state; strain energy

doi: http://dx.doi.org/10.22141/1608-1706.6.18.2017.121184

Введение

Эндопротезирование тазобедренного сустава является одним из самых распространенных видов оперативного вмешательства при лечении больных с дегенеративно-дистрофическими поражениями, что обеспечивает в большинстве случаев получение положительных результатов, восстановление двигательных возможностей, возвращение к трудовой деятельности [3]. В то же время примерно в 5 % случаев возникает необходимость ревизии из-за осложнений в послеоперационный период. Наиболее частым среди них является асептическая нестабильность [2]. Среди мер по предупреждению подобных ситуаций многие авторы [1, 4, 5] указывают в первую очередь на совершенствование конструкций эндопротезов для обеспечения первичной прочной фиксации, в том числе за счет структурированной и рельефной поверхности, необходимость правильного положения в костном канале и рационального распределения нагрузки на кость, применение материалов с механическими характеристиками, близкими к свойствам кости, а также демпфирующих покрытий.

Необходимость всестороннего изучения влияния конструктивных решений на исход протезирования в условиях учета большого количества разнообразных факторов и показателей делает актуальным использование современных средств компьютерного моделирования (CAD) и конечно-элементного анализа (CAE). Их применение дает возможность до выполнения операции прогнозировать ее последствия, оперативно оценивать различные варианты для обос–нованного выбора наиболее приемлемого. Поэтому в настоящее время компьютерные технологии играют все более заметную роль в ортопедии, имплантологии и других прикладных областях, что привело к появлению большого количества исследований, в частности [6–9] и многих других. В сочетании с компьютерной томографией (КТ) [10] возможности этих технологий существенно расширяются [11–13]. Как отмечено в монографии [14], они выходят за рамки только лишь детального биомеханического обоснования на стадии предоперационного планирования. Не менее важно принятие адекватных решений, а также прогнозирование ближайших и отдаленных последствий уже в послеоперационный период — путем анализа модели с изменениями, вносимыми в процессе наблюдения за пациентом. Настоящая работа также ориентирована на использование подобного подхода.

Цель исследования состоит в анализе напряженно-деформированного состояния имплантата и прилегающей зоны кости под действием физиологической нагрузки на различных стадиях восстановительного периода. Объектом рассмотрения является бедренный компонент эндопротеза тазобедренного сустава в виде трабекулярно-бионической ножки Physiohip, внедренной в бедренную кость.

Материалы и методы

Работа выполнена при участии инжиниринговой компании LASSO Ingenieurgesellschaft mbH, которая имеет обширный опыт моделирования и анализа разнообразных объектов сложной конфигурации. Преимущество использованного подхода состоит в двоякой комбинации технологий CAD/CAE и КТ — для построения геометрической модели и для описания механических свойств костной ткани.

Трехмерная геометрическая модель опорно-двигательного аппарата нижней конечности построена в среде препроцессора ANSA, представляющего собой мощный программный комплекс геометрического и конечно-элементного моделирования, с развитыми средствами автоматизации разработки, а также широкими возможностями обмена данными с другими CAD/CAE-пакетами [15]. Полная модель состоит из показанных на рис. 1А моделей костей, скрепленных мышцами и сухожилиями. Изучается механическое поведение части сборки, моделирующей бедренную кость с установленным эндопротезом Physiohip (рис. 1Б, В). Особенностью этого имплантата является большая площадь поверхности для обеспечения надежной фиксации за счет прорастания костной ткани. Условия нагружения соответствуют положению равновесия пациента на одной ноге.

Геометрическая модель, преобразованная в конечно-элементную структуру, экспортирована в универсальный CAE-пакет ABAQUS/Standard для выполнения расчетов. Непосредственно анализу предшествует подготовка расчетной схемы, включающая, помимо конечно-элементного разбиения модели, определение свойств материалов, задание условий закрепления и нагружения, а также выбор параметров вычислительного процесса.

Материал эндопротеза — титановый сплав, представляющий собой однородный изотропный материал. Для описания его упругих свойств достаточно задать две характеристики — модуль упругости E = 1,1 × 105 МПа и коэффициент Пуассона ν = 0,3. Сложнее обстоит дело с костной тканью, механические свойства которой характеризуются неоднородностью и существенной анизотропией [16]. Поэтому получение достоверных численных данных о взаимодействии имплантата с костью возможно только при наличии адекватной модели материала кости.

Для описания механических свойств костной ткани используется модель неоднородной упругой ортотропной среды, характеристики которой определяются индивидуально для каждого конечного элемента (КЭ), включая направления главных осей ортотропии, на основе изложенной в [13] методики. С целью определения материальных свойств in vivo используются данные о плотности костной ткани, полученные посредством КТ. Построение модели осуществляется в два этапа.

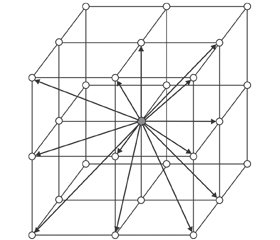
Первый этап состоит в выявлении и фиксации главных направлений ортотропии в пределах каждого КЭ кости. Подход основан на экстремальных свойствах модулей упругости вдоль главных осей. При этом подразумевается, что объемная структура уже создана компьютерным томографом, который представляет поля плотности КТ-изображения на дискретной сетке вокселов. Для отыскания главных направлений используется алгоритм «пространственной звезды», в котором исследуется феноменологическая картина изменения плотности костной ткани в окрестности изучаемой точки. С этой целью анализируются изменения КТ-чисел вдоль 13 направлений, проходящих через данную точку. Изменение плотности в каждом из направлений оценивается сопоставлением значений КТ-числа для пары вокселов томограммы, лежащих на одной прямой вместе с данным. 26 вокселов, смежных с данным, как показано на рис. 2, образуют 13 пар и определяют 13 направлений поиска.

Направление с наименьшим градиентом плотности принимается за главное направление ортотропии, соответствующее наибольшему модулю упругости; направление наибольшего градиента отождествляется с осью наименьшего модуля упругости [13]. Тогда главное направление, соответствующее промежуточному модулю, отыскивается векторным умножением ортов найденных ранее двух направлений. Ориентация главных осей первоначально определяется отдельно для каждого воксела. Вместе с тем в общей совокупности эти результаты обнаруживают согласованность. В частности, в диафизарной области ось наибольшего модуля имеет приблизительно проксимально-дистальное направление, ось наименьшего модуля ориентирована по толщине диафиза, а ось промежуточного модуля — вдоль контура поперечного сечения, то есть в окружном направлении.

Задача второго этапа состоит в вычислении значений 9 упругих констант относительно системы координат, совмещенной с найденными на первом этапе главными направлениями ортотропии. Для подсчета на основании данных КТ о распределении плотности костной ткани возможно использование соотношений [17], которые для кортикальной кости представляются формулами:

а для спонгиозной имеют вид:

где E1, E2, E3 — главные модули ортотропной упругости (в порядке возрастания), измеренные в МПа; CT — КТ-число, выраженное в единицах Хаунсфилда (Hu).

Как отмечено в [13], справедливость этих формул ограничена диапазонами КТ-чисел CT ∈ [1000,1826] для (1) и CT ∈ [–25,298] для (2). Поэтому была предложена единая аналитическая зависимость в виде суперпозиции экспоненты с линейной функцией:

Такая аппроксимация позволяет с приемлемой точностью описать упругие свойства обеих костных структур и обеспечивает непрерывный переход между ними. Входящие в (3) константы найдены путем обработки экспериментальных данных и представлены в табл. 1 [13].

Для полного описания ортотропных механических свойств относительно главных направлений, помимо трех модулей упругости E1, E2, E3, требуются еще значения трех модулей сдвига G12, G13, G23 и трех коэффициентов поперечного сжатия ν12, ν13, ν23. Непосредственное определение 6 оставшихся констант по распределению КТ-плотности затруднительно, поэтому их приближенное отыскание основывается на ограничениях, следующих из свойств симметрии и положительной определенности матрицы коэффициентов жесткости, а также из соотношений в виде неравенств для выбранного способа упорядочивания главных направлений [13]:

Упомянутые ограничения позволяют построить систему неравенств и в результате найти приближенные значения ν₁₂, ν₁₃, ν₂₃ за счет максимального сужения диапазонов их возможных значений [13]. При этом еще три коэффициента поперечного сжатия определяются из условий ν₂₁ = ν₁₂E₂ / E₁, ν₃₁ = ν₁₃E₃ / E₁, ν₃₂ = ν₂₃E₃ / E₂.

Для отыскания модулей сдвига предложена формула [13] (суммирования нет):

Строго говоря, это не вписывается в концепцию 9 независимых упругих констант ортотропной среды. С другой стороны, такой подход является вынужденным, а с учетом удовлетворительного экспериментального подтверждения [13] может рассматриваться как приближенный способ подсчета упругих констант.

Описанный двухступенчатый алгоритм применяется индивидуально ко всем вокселам КТ-изображения бедра. В результате ориентация главных осей и величины упругих констант для каждого КЭ модели кости определяются усреднением по всем вокселам в пределах данного элемента. Существенным аспектом при этом является идентификация всех вокселов, относящихся к конкретному элементу. Процедура поиска иллюстрируется рис. 3 на примере тетраэдрального КЭ. Расстояние от рассматриваемой точки до каждой из боковых граней тетраэдра, нумерация которых соответствует номеру противолежащей вершины, может быть подсчитано по формуле:

где nk — вектор единичной внешней нормали к грани с номером k; rl — радиус-вектор одной из вершин грани; rV — радиус-вектор воксела относительно глобальной системы отсчета (рис. 3А). В частности, согласно обозначениям на рис. 3:

В свою очередь, нормали к граням можно выразить с помощью векторного произведения. Например:

где F1 — площадь 1-й грани. Аналогично определяются величины с номерами k = 2, 3, 4.

Принципиальным является то, что проверяются только вокселы, координаты которых попадают в интервалы между min и max координатами всех узлов элемента. Другими словами, испытуемый воксел всегда лежит внутри параллелепипеда, очерченного вокруг данного КЭ шестью координатными плоскостями, положение которых определяется диапазонами координат вершин элемента (рис. 3Б).

Вне зависимости от порядка нумерации вершин конкретного КЭ существует закономерность, позволяющая однозначно судить о местоположении данного воксела: если все расстояния (6) имеют одинаковый знак, то воксел внутри элемента; в противном случае воксел вне элемента.

Таким образом, изложенная процедура дает возможность задать необходимые для анализа модели механические свойства костной ткани на основе данных КТ.

При задании условий нагружения и закрепления принято во внимание, что нижняя часть ноги не является предметом анализа, поэтому она заменена жесткой балкой, реализующей корректное положение колена. Аналогично нагрузочное воздействие таза и верхней части тазобедренного сустава представлено набором сил, проходящих через центр сферической головки, при этом учтено предварительное напряжение мышц, соответствующее положению равновесия на одной ноге [18, 19]. Равнодействующая этих сил составляет примерно 2000 Н. Указанные упрощения, не внося существенных погрешностей, позволяют сосредоточить внимание на анализе бедренной кости с внедренным имплантатом.

Выбор густоты конечно-элементного разбиения модели обоснован согласованием с погрешностью в пределах 5 % численных и экспериментальных данных для задачи о сжатии испытательного образца из диафиза [13]. В результате общее число элементов расчетной модели составило 688 319, а число узлов — 181 973.

Задача о совместном деформировании кости и ножки протеза ставится как контактная, что делает ее конструктивно нелинейной. Выбран тип контакта «поверхность с поверхностью». При этом для случая краткосрочной стабилизации предполагается скользящий контакт с коэффициентом трения 0,01. Для случая долгосрочной стабилизации контакт моделируется как полный (двусторонний) на соответствующих участках поверхности ножки.

Все расчеты выполнялись в CAE-системе ABAQUS/Standard в два шага нагружения. На первом шаге устанавливается положение контакта, а на втором прикладывается полная нагрузка.

Результаты и обсуждение

Ниже представлены некоторые результаты расчетов. Напряжения на контактных поверхностях имплантата характеризуют степень его фиксации в кости. Нормальные напряжения представлены в виде полей контактных давлений (показана только наружная поверхность эндопротеза). Как видно на рис. 4, наибольшие значения контактного давления на стадии краткосрочной стабилизации наблюдаются в нижней части ножки эндопротеза.

Максимальные касательные напряжения на этой стадии, когда контакт скользящий, достигают относительно небольших значений и показаны на рис. 5А. В случае долгосрочной стабилизации контакт моделируется как двусторонний, что означает полное сцепление имплантата с костью на поверхностях их соприкосновения. Поэтому на данной стадии значения максимальных касательных напряжений выше, с локализацией по-прежнему в нижней части ножки, что иллюстрирует рис. 5Б. При этом наблюдаются отдельные области с небольшими отрицательными значениями контактного давления, показанными на рис. 6, что соответствует наличию растягивающих напряжений. Виды А и Б на рис. 4 и 6 демонстрируют модель эндопротеза в разных ракурсах.

В качестве количественной характеристики уровня напряженного состояния кости у поверхности имплантата выбрано первое главное напряжение. Такой выбор обусловлен тем, что для костной ткани наибольшую опасность представляют растягивающие напряжения. Критерий наибольших нормальных напряжений [20] пригоден для оценки прочности тел из хрупких материалов, прочность которых при растяжении заметно ниже, чем при сжатии.

Показанные на рис. 7 распределения свидетельствуют о том, что в случае долгосрочной стабилизации доля внешней нагрузки, воспринимаемой костью у поверхности имплантата, заметно снижается по сравнению с краткосрочным вариантом. Кроме того, полученные значения далеки от предела прочности бедренной кости при растяжении, который составляет 129–148 МПа [21]. Таким образом, при заданных характере и величине внешней физиологической нагрузки прочность костной ткани вблизи эндопротеза гарантирована.

Удобной мерой степени нагруженности в той или иной части упруго деформированного тела является величина потенциальной энергии деформации, то есть упругой энергии, накапливаемой в изучаемом объеме. Для подсчетов были выделены 84 сектора, образующие 7 слоев (нумерация сверху вниз), по 12 секторов в верхней части конечно-элементной модели кости, как показано на рис. 8. В каждом слое выполнено суммирование по секторам медиальной, латеральной, антериорной и постериорной областей. Результаты приведены на рис. 9 и 10 для кости с эндопротезом на стадии долгосрочной стабилизации и для целой кости при идентичных условиях нагружения.

Обращает на себя внимание, что наибольшее расчетное значение энергии деформации в положении равновесия на одной ноге для кости с имплантатом ниже, чем для природной неповрежденной кости, что само по себе свидетельствует о достаточной прочности. Кроме того, как следует из гистограмм, распределения накопленной упругой энергии в зонах 1–7 природной кости и кости с имплантатом выглядят подобным образом. Это означает, что эндопротез Physiohip обеспечивает распределение внешней нагрузки, близкое к естественному, что является его несомненным достоинством.

Выводы

Выполненные исследования позволили получить количественные и качественные оценки механических аспектов взаимодействия трабекулярно-бионической ножки Physiohip с костью в условиях восприятия физиологической нагрузки частного вида.

Показано, что с течением времени происходит перераспределение нагрузки между имплантатом и костью так, что нагруженность кости снижается. При этом и для краткосрочного, и для отдаленного периодов требования прочности кости выполнены.

Обнаружено, что характер передачи нагрузки на кость через ножку эндопротеза Physiohip при долгосрочной стабилизации близок к физиологическому.

В целом в сочетании с данными клинических наблюдений эти сведения дают основания считать трабекулярно-бионическую ножку Psysiohip довольно эффективным средством эндопротезирования тазобедренного сустава при дегенеративно-дистрофических заболеваниях. Это является результатом научных поисков инертных и родственных материалов и конструкций.

В перспективе для всесторонней оценки возможностей ножки Physiohip представляется целесообразным выполнить моделирование и анализ взаимодействия данного имплантата с костью при других видах физиологических нагрузок, в частности, для случая подъема по лестнице.

Конфликт интересов. Авторы заявляют об отсутствии какого-либо конфликта интересов при подготовке данной статьи.

Список литературы

1. Гайко Г.В. Пористе титанове та титан-гідроксіапатитне покриття для безцементного ендопротеза кульшового суглоба (експериментальне дослідження) / Г.В. Гайко, В.М. Підгаєцький // Ортопедия, травматология и протезирование. — 2008. — № 4. — C. 47-53.

2. Гайко Г.В. Діагностика асептичної нестабільності компонентів ендопротеза кульшового суглоба в ранні терміни / Г.В. Гайко [та ін.] // Вісник ортопедії, травматології та протезування: український науково-практичний журнал. — К.: Атлант, 2008. — № 3. — C. 5-9.

3. Корж Н.А. Проблема эндопротезирования суставов в Украине и пути ее решения / Н.А. Корж, В.А. Филиппенко, В.А. Танькут // Ортопедия, травматология и протезирование: Науч.-практ. журн. / Ин-т патологии позвоночника и суставов им. проф. М.И. Ситенко, Укр. ассоц. ортопедов-травматологов. — Харьков, 2008. — № 2. — C. 5-9.

4. Косяков О.М. Шляхи профілактики асептичної нестабільності стегнового компоненту ендопротеза кульшового суглоба / О.М. Косяков, О.А. Бур’янов, В.К. Бондар // Літопис травматології та ортопедії. — К., 2012. — № 1/2. — C. 190-192.

5. Филиппенко В.А. Эволюция проблемы эндопротезирования суставов / В.А. Филиппенко, А.В. Танькут // Международный медицинский журнал: ежеквартальный научно-практический журнал. — Харьков, 2009. — Т. 15, № 1. — C. 70-74.

6. Helwig P. et al. Finite element analysis of four different implants inserted in different positions to stabilize an idealized trochanteric femoral fracture // Injury. — 2009. — Vol. 40, Issue 3. — Р. 288-295.

7. Helwig P. et al. Finite element analysis of a bone-implant system with the proximal femur nail // Technology and Health Care. — 2006. — Vol. 14, № 4–5. — Р. 411-419.

8. Чуйко А.Н., Олейник А.В. О биомеханике нижней челюсти человека при протезировании несъемными протезами // Российский журнал биомеханики. — 2009. — № 1. — С. 79-94.

9. Lvov G.I. et al. Computer-Aided Design of the Shinbone Osteosyntesis // Proceedings of ICTE 2011 II International Conference on Tissue Engineering. — Lisbon, Portugal: Ist Press, 2011. — Р. 181-188.

10. Экспериментальные методы в биомеханике: учеб. пособие / Ю.И. Няшин, Р.М. Подгаец. — Пермь: Изд-во ПГТУ, 2008. — 400 с.

11. Чуйко А.Н. О возможностях биомеханического анализа с использованием современных компьютерных технологий. — Краснодар: ДенталЮг, 2009. — № 6. — С. 50-55.

12. Limbert G. et al. Interaction of a dental implant with the trabecular bone microstructure. A μCT-based three-dimensional finite element study using the Materialise Software Suite // Mimics Innovation Award. — 2007. — Р. 1-14.

13. Schneider R. et al. Inhomogeneous, orthotropic material model for the cortical structure of long bones modelled on the basis of clinical CT or density data // Computer Methods in Applied Mechanics and Engineering. — 2009. — Vol. 198, Issues 27–29. — Р. 2167-2174.

14. Чуйко А.Н., Шинчуковский И.А. Биомеханика в стоматологии. — Харьков: Форт, 2010. — 468 с.

15. http://www.lasso.de/index.php?id=10&L=3

16. Моделирование в биомеханике: учеб. пособие / П.И. Бегун, П.Н. Афонин. — М.: Высш. шк., 2004. — 390 с.

17. Rho J.Y. et al. Relations of mechanical properties to density and CT numbers in human bone // Medical Engineering and Physics. — 1995. — № 17. — Р. 347-355.

18. Bergmann G. et al. Hip contact forces and gait patterns from routine activities // J. Biomech. — 2001. — Vol. 34(7). — Р. 859-871.

19. Heller M.O. et al. Musculo-skeletal loading conditions at the hip during walking and stair climbing // J. Biomech. — 2001. — Vol. 34(7). — Р. 883-893.

20. Писаренко Г.С., Лебедев А.А. Деформирование и прочность материалов при сложном напряженном состоянии. — К.: Наук. думка, 1976. — 426 с.

21. Lindahl O., Lindgren A. Cortical bone in man. II. Variation in tensile strength with age and sex // Acta Оrthopaed. Scand. — 1967. — Vol. 38. — Р. 141-147.