Мобильная версия

Журнал «Травма» Том 20, №2, 2019

Обоснование формы резьбового элемента вертлужного компонента эндопротеза тазобедренного сустава

Авторы: Лоскутов А.Е.(1), Панченко С.П.(2), Олейник А.Е.(1), Ковбаса Е.А.(1), Губарик А.В.(3)
(1) — ГУ «Днепропетровская медицинская академия МЗ Украины», г. Днепр, Украина
(2) — ГУ «Приднепровская академия строительства и архитектуры», г. Днепр, Украина
(3) — КУ «Днепропетровская областная клиническая больница им. И.И. Мечникова», г. Днепр, Украина

Рубрики: Травматология и ортопедия

Разделы: Клинические исследования

Актуальність. Ацетабулярну реконструкцію із застосуванням вертлюгових компонентів, що загвинчуються, слід вважати найбільш перспективною з позиції досягнення тривалої стабільності імплантату, в тому числі у випадках складних, нестандартних та ревізійних втручань. Однак причини розвитку нестабільності конструкції залишаються недостатньо висвітленими, що свідчить про актуальність пошуку рішень у площині біомеханічних досліджень мікровзаємодії в зоні контакту «ендопротез/кістка». Мета: визначення раціональних параметрів геометрії різьбового елементу чашки ендопротезу кульшового суглоба, що загвинчується. Матеріали та методи. Створено кінцевоелементні розрахункові моделі, що розрізняються за формою та розмірами різьбового елемента чашки ендопротеза, а також за величиною кута нахилу конуса чашки відносно вертикальної вісі. Критерієм ефективності різьбового элемента були обрані значення максимальних напружень у кістковому масиві. Дослідження виконувалось у середовищі програмного комплекса ANSYS. Результати та обговорення. Найбільш ефективною з точки зору розподілення локальних напружень у зоні контакту «ендопротез/кістка» є модель різьбового елемента, поперечний переріз якого представлено прямокутним трикутником, що спирається своїм катетом на кістковий масив. Цей результат є справедливим як при спиранні корпуса чашки на кістку, так і при його відсутності. Зміна кута нахилу утворюючої чашки до 15° призвела до різноспрямованої зміни напружено-деформованого стану в кістковому масиві — збільшення напружень у моделях 2 і 3 та зниження у моделі 1 (спирання гіпотенузою на кістковий масив). При оцінці впливу величини кута нахилу утворюючої (0–15°) на напружено-деформований стан для моделі 1 найменші пікові навантаження було виявлено при 5–15° кутах нахилу. Наведена якісна картина напруженого стану тазової кістки є неоднорідною та потребує подальших досліджень. Висновки. Обґрунтування раціональної геометрії конструкції вертлюгового компоненту, що загвинчується, слід реалізовувати в площині дослідження контактних взаємодій вузла «ендопротез/кістка», що об’єктивізує біомеханічну картину в зоні контакту. Визначено, що найбільш ефективною є модель різьбового елементу, поперечний переріз якого представлено прямокутним трикутником, що спирається катетом на кістковий масив, що доцільно враховувати при виборі конструкції імплантату.

Актуальность. Ацетабулярная реконструкция с применением ввинчивающихся вертлужных компонентов представляется наиболее перспективной с позиции достижения длительной стабильности имплантата, в том числе в случаях сложных, нестандартных и ревизионных вмешательств. Однако причины развития нестабильности конструкции остаются недостаточно определенными, что свидетельствует об актуальности поиска решений в плоскости биомеханических исследований микровзаимодействий в зоне контакта «эндопротез/кость». Цель: определение рациональных параметров геометрии резьбового элемента ввинчивающейся чашки эндопротеза тазобедренного сустава. Материалы и методы. Построены конечноэлементные расчетные модели, отличающиеся формой и размерами резьбового элемента чашки эндопротеза, а также величиной угла наклона конуса чашки относительно вертикальной оси. Критерием эффективности резьбового элемента были выбраны величины максимальных напряжений в костном массиве. Исследование выполнялось в среде программного комплекса ANSYS. Результаты. Наиболее эффективной с точки зрения распределения локальных нагрузок в зоне контакта «эндопротез/кость» является модель резьбового элемента, поперечное сечение которого представлено в виде прямоугольного треугольника, опирающегося своим катетом на костный массив. Этот результат справедлив как при опоре корпуса чашки на кость, так и при ее отсутствии. Изменение угла наклона образующей чашки до 15° привело к разнонаправленному изменению напряженно-деформированного состояния в костном массиве — увеличению напряжений у моделей 2 и 3 и снижению у модели 1 (опора гипотенузой на костный массив). При оценке влияния величины угла наклона образующей (0–15°) на напряженно-деформированное состояние для модели 1 наименьшие пиковые нагрузки выявлены при 5–15° углах наклона. Представленная качественная картина напряженного состояния тазовой кости в ходе имплантации является неоднородной и требует дальнейших исследований. Выводы. Обоснование рациональной геометрии конструкции ввинчивающегося компонента эндопротеза следует реализовывать в плоскости оценки контактных взаимодействий узла «эндопротез/кость», что объективизирует биомеханическую картину в зоне контакта. Выявлено, что наиболее эффективной является модель резьбового элемента, поперечное сечение которого представлено в виде прямоугольного треугольника, опирающегося катетом на костный массив, что целесообразно учитывать при выборе конструкции имплантата.

Background. Acetabular reconstruction with threaded cups remains promising in achieving long-term stability of the implant both in cases of complicated and revision total hip replacements. Nevertheless, the causes of cup instability still remain unclear that makes biomechanical research of “endoprosthesis/bone” microinteractions of great interest. The purpose was to determine optimal parameters of threaded element geometry of threaded acetabular component of total hip endoprosthesis. Materials and methods. Finite element models were created, they varied in terms of cup threaded element geometry (model 1 — threaded element with right-angled triangle transverse section resting upon the bone with its hypotenuse; model 2 — threaded element with right-angled triangle transverse section resting upon the bone with its cathetus; model 3 — threaded element with isosceles triangle transverse section resting upon the bone with one of its equal sides) and cup cone inclination angle (with the angle range of 0–15°). Maximal tensile forces in bone were determined as the criteria for effectiveness. The research was conducted with ANSYS software package. Results. It was found that threaded element model with right-angled triangle transverse section resting upon the bone with its cathetus seems to be the most effective in terms of local tension distribution in “the cup/bone” interspace. This result is valid both for conditions when the cup cone is/isn’t resting upon bone. Increasing the cup cone inclination angle up to 15° led to multidimensional changes in bone stress strain state: increasing peak forces in model 2 and model 3 and decreasing in model 1 (the triangle leans on the bone with its hypotenuse). Additionally, the influence of the cup cone inclination degree on the stress strain state was evaluated for the model 1. So, the least peak forces for the threaded element with right-angled triangle transverse section res-ting upon the bone with its hypotenuse were assessed with cup cone inclination angles of 5–15°. Revealed qualitative patterns of pelvic bone stress strain state during implantation represent heterogeneity and require further research. Conclusions. Threaded cup geometry grounding should be implemented through the assessment of biomechanical interactions of “the cup/bone” interspace. It was found that threaded element model with right-angled triangle transverse section seems to be the most effective that is advisable to take into conside-ration when choosing acetabular components.

Ключевые слова

кульшовий суглоб; ендопротез; вертлюговий компонент; різьбовий елемент; метод кінцевих елементів; напружено-деформований стан

тазобедренный сустав; эндопротез; вертлужный компонент; резьбовой элемент; метод конечных элементов; напряженно-деформированное состояние

hip joint; endoprosthesis; acetabular component; threaded element; finite element method; stress strain state

doi: http://dx.doi.org/10.22141/1608-1706.2.20.2019.168021

Введение

Прогрессивный рост количества операций тотального эндопротезирования тазобедренного сустава (ТЭТС) по всему миру обусловливает увеличение доли ревизионных вмешательств, несмотря на существенные прогрессивные научно-технические разработки в отрасли [17, 18, 20]. Так, по данным регистров эндопротезирования Европы и США [2, 4–6, 9, 11–13], соотношение первичного и ревизионного эндопротезирования тазобедренного сустава в мире составляет 5 : 1, а доля ревизионных вмешательств колеблется от 15 до 24 %. Следует отметить, что 70 % всех ревизий выполняется из-за нестабильности вертлужного компонента, ведущая причина развития которой — несоответствие имплантата морфоимплантационным характеристикам вертлужной впадины, а также изменение структуры костных элементов впадины в процессе функционирования эндопротеза [17, 20, 11–13]. Среди возможных вариантов ацетабулярной реконструкции в ходе ТЭТС бесцементные ввинчивающиеся вертлужные компоненты (ВК) представляются наиболее перспективными с позиции достижения длительной стабильности имплантата, в том числе в случаях сложных, нестандартных и ревизионных вмешательств [1, 10, 14, 15, 18]. Будучи впервые примененным ортопедами в первой трети XX века, принцип бесцементной фиксации вертлужного компонента за счет ввинчивания претерпел существенное развитие благодаря фундаментальным разработкам Willis (1937), McKee (1951), Сиваша (1957), Mittelmeier (1963) и нашел свое продолжение в богатом разнообразии конструкций и покрытий [7, 8, 15, 17, 18, 20]. При этом и современные образцы конструкций демонстрируют обнадеживающие результаты выживаемости [1, 3, 10, 14, 15]. Следует отметить, что причины развития нестабильности при использовании ввинчивающегося вертлужного компонента остаются недостаточно определенными, что свидетельствует об актуальности поиска решений в плоскости биомеханических исследований микровзаимодействий в зоне контакта «эндопротез/кость» [3, 10, 15]. На сегодняшний день ряд исследователей считают, что ведущая роль в достижении адекватной первичной фиксации, создании благоприятных биомеханических условий для остеоадгезии и остеоинтеграции, а следовательно, для формирования отдаленной стабильности имплантата, наряду с формой сечения корпуса компонента, принадлежит дизайну конструкции резьбы и ее элементов [3, 10, 15, 16, 18].

Целью работы является определение рациональных параметров геометрии резьбового элемента ввинчивающейся чашки эндопротеза тазобедренного сустава.

Материалы и методы

Для оценки влияния геометрии резьбового элемента чашки на напряженно-деформированное состояние системы «кость — чашка» были построены различные расчетные модели, различающиеся формой и размерами резьбового элемента чашки эндопротеза, а также величиной угла наклона конуса чашки относительно вертикальной оси. При этом все расчетные модели строились в соответствии с реальными размерами резьбового элемента ввинчивающейся чашки.

Исследование выполнялось в среде программного комплекса, основанного на методе конечных элементов (ПК ANSYS). Для рационального использования ресурса комплекса форма чашки должна была быть симметричной, что позволило рассматривать отдельный резьбовой элемент чашки. При этом криволинейная форма резьбового элемента была заменена на прямолинейную.

Расчетная модель системы «кость — чашка» представлена двумя элементами, один из которых соответствует резьбовому элементу чашки эндопротеза тазобедренного сустава, второй — костному массиву, в который врезан резьбовой элемент. Оба элемента представляют собой правильные прямые четырех-угольные призмы. При этом призма, соответствующая элементу эндопротеза, дополнена вставкой, имитирующей резьбу. Призма, соответствующая кости, дополнена желобом под вставку. Форма вставки определяется формой поперечного сечения резьбы. В данном исследовании рассматривается три варианта сечения резьбы треугольной формы: 1) прямоугольный треугольник, который опирается на костный массив своей гипотенузой (рис. 1а), прямоугольный треугольник, опирающийся катетом (рис. 1б), и равнобедренный треугольник c осью симметрии в направлении х, опирающийся на кость одной из равных сторон (рис. 1в). В соответствии с этим были построены три расчетные модели. Моделирование осуществлялось таким образом, чтобы общие грани элементов эндопротеза и костного массива полностью соответствовали друг другу.

На первом этапе исследовалось влияние геометрии поперечного сечения резьбового элемента чашки эндопротеза тазобедренного сустава на характер и величину возникающих в костном массиве внутренних усилий и деформаций в случае отсутствия опоры корпуса эндопротеза на костный массив (рис. 2), при этом решалась контактная задача.

Так как рассматривалась упрощенная модель системы «кость — чашка», то размеры элементов задавались произвольно, однако определяющим был размер вставки, моделирующей резьбу. В частности, размеры модели элемента чашки и костного массива принимались равными: L1 — 10 мм, L2 — 10 мм, высота резьбового элемента эндопротеза h — 4,5 мм, основание резьбового элемента эндопротеза t — 3 мм, длина зубца — 10 мм. Соответственно, поперечный размер призм также составлял 10 мм.

Материал элементов модели предполагался упругий, однородный, изотропный. Для элемента чашки механические характеристики соответствовали титану: модуль нормальной упругости (Юнга) E = 106 ГПа, коэффициент Пуассона υ = 0,3; для костного массива: модуль Юнга E = 0,1 ГПа, коэффициент Пуассона υ = 0,2, что соответствует усредненным показателям для спонгиозной костной ткани.

Поскольку рассматривалась не вся конструкция системы «кость — чашка», а только ее часть, на грани модели накладывались соответствующие граничные условия. Для резьбового элемента модели эндопротеза на внешней грани призмы AYZ запрещены все углы поворота и перемещения, кроме перемещения вдоль вертикальной оси Y. Для модели костного массива вдоль правой грани призмы BYZ заданы условия абсолютно жесткого защемления.

В качестве нагрузки задавалось равномерно распределенное давление, действующее на верхней грани части модели, соответствующей части резьбового элемента. Нагрузка задавалась, исходя из напряжений, возникающих в зоне контакта реального эндопротеза при величине силы, действующей на эндопротез, равной одной трети от массы тела человека, P = 270 Н.

На рис. 3 представлены расчетные схемы в зависимости от вида резьбы.

Расчеты производились с использованием схем, построенных на базе 4-узловых конечных элементов в форме тетраэдра с 6 степенями свободы в каждом узле. Для разбиения моделей на конечные элементы использовался автоматический генератор сеток в рамках ПК ANSYS. При этом рассматривалась контактная задача двух тел в рамках теории упругости. Поэтому вдоль общих для двух моделей граней заданы условия контактного взаимодействия, а также наложено условие максимального линейного размера конечного элемента, равного 1 мм.

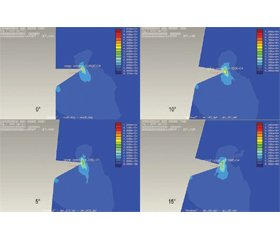
Результаты и обсуждение

Для исследования влияния геометрии резьбового элемента имплантата на характер фиксации оценивалось напряженно-деформированное состояние (НДС) костной ткани. В качестве критерия эффективности резьбового элемента были выбраны величины максимальных напряжений в костном массиве, которые приведены в табл. 1.

При получении результатов расчетов для удобства в каждой модели было проведено дополнительное поперечное (в плоскости) XoY сечение через середину призмы. Поэтому приведенные результаты соответствуют величинам напряжений в этом сечении (рис. 4).

В соответствии с данными, представленными в табл. 1, наибольшие максимальные напряжения возникают у модели 1 (опора резьбового элемента на гипотенузу), их величина составила 6,47 МПа. Наименьшими по величине оказались максимальные напряжения у модели 2 (опора на катет), которые были на 43 % меньше, чем у модели 1, и равны 3,66 МПа. У модели 3 (резьбовой элемент в виде равнобедренного треугольника) максимальные напряжения составили 4,78 МПа, что оказалось меньше, чем у модели 1, на 26 % и больше, чем у модели 2, на 31 %.

Анализ распределения напряжений в костной ткани показал, что у всех моделей напряженное состояние является существенно неоднородным. При этом имеет место выраженная зона концентрации напряжений в вершине моделирующего резьбу треугольника. Здесь необходимо отметить, что приведенные величины напряжений возникают в месте концентрации, в частности в одном узле. Характер распределения напряжений в костной ткани приведен на рис. 5.

Таким образом, на основании анализа полученных величин напряжений можно сделать вывод, что наиболее эффективной с точки зрения прочности при отсутствии опоры чашки на костный массив является модель 2 (опора резьбового элемента на катет), максимальные напряжения в которой оказались наименьшими среди рассматриваемых моделей системы «кость — чашка».

На втором этапе исследовалось влияние геометрии резьбового элемента вертлужного компонента эндопротеза на НДС системы «кость — чашка» для случая опоры корпуса эндопротеза на костный массив (при наличии угла наклона образующей конуса).

Для выполнения этого исследования были построены расчетные модели, которые отличались, как и ранее, только геометрией резьбового элемента. При этом методика построения расчетных моделей оставалась прежней. Кроме того, основные геометрические размеры моделей, а также физико-механические свойства материалов моделей также не изменялись. Отличие за

Список литературы

1. Cameron H.H. Techniques of insertion and results with the threaded acetabular component / H. H. Cameron, T. McTighe // Surg. Rounds Orthop. — 1989. — Vol. 98, № 1. — P. 22-28.

2. Danish Hip Arthroplasty Register // Annual Report. — 2004 [Электронный ресурс]. http://www.dhr.dk.

3. Modes of failure of a threaded acetabular cup. A radiographic study with EBRA of 42 revised cups / T. Ilchmann, S. Neher, F. Maurer, K. Weise // Inter. Orthop. (SICOT). — 2007. — Vol. 31. — P. 211-216.

4. National Joint Registry for England, Wales and Northern Ireland // 10th Annual Report. — 2013 [Электронный ресурс]. http://www.njrcenter.org.uk.

5. National Joint Registry for England, Wales and Northern Ireland // 8th Annual Report. — 2010 [Электронный ресурс]. http://www.njrcenter.org.uk.

6. Registro Ortopedico Lombardo Protesi. Sesto Raporto — Novembre 2012 [Электронный ресурс]. — Режим доступа: http://www.sanita.regione.lombardia.it/es.

7. Salvi A.E. The innovative Sivash artificial total hip joint / A.E. Salvi, G. Grappiolo, S.A. Hacking // Univers. Pennsylvania Orthop. J. — 2010. — Vol. 20. — P. 151-153.

8. Sivash K.M. Alloplasty of the hip joint. A laboratory and clinical study / K.M. Sivash // Central Institute for Traumatology and Orthopaedics. — Moscow: Medical Press, 1967.

9. Slovakian Arthroplasty Register 2010 [Электронный ресурс]. http://www.efort.org.

10. Survivorship of rough-surfaced threaded acetabular cups 382: consecutive primary Zweymiiller cups followed for 0.2–12 years / C.P. Delaunay, A.I. Kapandji // Acta Orthop. Scand. — 1998. — Vol. 69, № 4. — P. 379-383.

11. Swedish Hip Arthroplasty Register // Annual Report. — 2010 [Электронный ресурс]. http://www.shpr.se/en.

12. The Geneva Hip Arthroplasty Registry // Annual report. — 2010 [Электронный ресурс]. http://www.efort.org.

13. The Norwegian Arthroplasty Register // Report June. — 2010 [Электронный ресурс]. http://www.haukeland.no.

14. Threaded acetabular components for primary and revision total hip arthroplasty / J.A. Shaw, J.H. Bailey, A. Bruno, R.B. Greer // J. Arthroplasty. — 1990. — Vol. 5, № 3. — P. 202-215.

15. Threaded acetabular components: design rationale and preliminary clinical results / T.H. Mallory, B.K. Vaughn [et al.] // Orthop. Rev. — 1988. — Vol. 17. — P. 305-311.

16. Witzel U. Three-dimensional stress analysis of threaded cups — a finite element analysis / U. Witzel, W. Rieger, H. Effenberger // Inter. Orthop. (SICOT). — 2008. — Vol. 32. — P. 195-201.

17. Загородний Н.В. Эндопротезирование тазобедренного сустава / Н.В. Загородний. — М.: ГЭОТАР-Медиа, 2012. — 704 c.

18. Лоскутов А.Е. Эндопротезирование тазобедренного сустава. — Днепропетровск: Лира, 2010. — 344 с.

19. Проблемы прочности в биомеханике: учеб. пособие для технич. и биол. спец. вузов / И.Ф. Образцов, И.С. Адамович, А.С. Барер и др.; под ред. И.Ф. Образцова. — М.: Высш. шк., 1988. — 311 с.: ил.

20. Тихилов Р.М. Руководство по эндопротезированию тазобедренного сустава / Под ред. Р.М. Тихилова, В.М. Шаповалова. — СПб.: РНИИТО им. Р.Р. Вредена, 2008. — 324 с.